锤式破碎机中单颗粒物料的最大破碎力研究

　　锤式破碎机具有破碎效率高，破碎能耗少等特点.它在矿山、建材、环保等行业中得到了广泛地应用。到目前为止.锤式破碎机的最大破碎力还没有一个理想的公式进行计算。国外有人根据碰撞理论和破碎力呈线性变化的观点。提出了最大破碎力Fmax等于二倍平均破碎力F１的公式。但是由于物料在实际破碎过程中，最大的破碎力与平均破碎力的比值并不是呈线性变化因而有必要对该机型的最大破碎力做进一步的探讨。

       
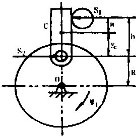
图1单顺粒物料破碎时力学摸型

　　1单颗粒物料破碎时最大破碎力的理论分析
　　锤式破碎机对物料的破碎过程可以看作是锤头与物料的碰撞过程.其力学模型如图1所示。为了便干研究。对其碰撞过程做如下几点假设:①在破碎过程中.物料与锤头碰撞是弹性正碰撇;②在碰撞前，锤头与转子同速转动;③在碰撞前，物料水平速度为零;④在碰撞处，忽略摩擦力和风阻等的影响。
　　根据上述假设和碰撞理论。可得如下方程：

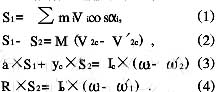
式中。mi为碰撞后.第i块物料的质量;M为锤头的质量;Vi为第i块物料碰撞后的分速度；V2c为碰撞前,锤头质心c处的线速度；
V2c=(R+yc)×ω；
ω为碰撞前。转子的角速度;ω1为碰撞后,转子的角速度;R为转子轴心到锤头销轴轴心间的距离;yc为锤头质心c到锤头轴轴心间的距离;ω2为碰撞前,锤头的角速度。根据假设可得:
ω2=ω1;
ω'2为碰撞后,锤头的角速度;V'2c.为碰撞后,锤头质心c处的线速度;
V'2c=R×ω'1+yc×ω'2
Io为转子系统对o轴的转动惯量;I为锤头对其质心轴的转动惯量;α1为第i块物料的速度Vi与碰撞方向的夹角;a为锤头打击点到锤头质心c间的距离;b为锤头打击点到销轴轴心间的距离;
b+ a+ yc;
S1为锤头与物料间的碰撞冲量;S2为锤头销轴间的碰撞反冲量。
    另外.根据牛顿的恢复系数K定义可知:

式中。t为冲击破碎时间,本文取t= 0.0015g.
　　同理，单颗粒物料破碎时，锤头对销轴的平均反冲力为：

　　在上式中.由干δ在破碎过程中与时间无关.当出现最大破碎力F1max时,可得:F1max=δ×F2max,式中。F2max为锤头对销轴的最大反冲击力。

　　2单颗粒物料破碎时最大破碎力的实验研究
　　为了测出单颗粒物料破碎时的最大破碎力.设计了直径400单排锤式破碎机.并在转子轴中部对称地粘贴4个电阻应变片。如图2所示。

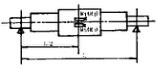
图２　锤式破碎机转子轴上布片图

　　并通过导线组成全桥测试电跟如图3所示。
　　根据上述测试方法。单颗粒物料破碎时.转子轴上的弯曲应变曲线如图4所示.

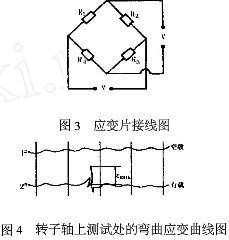
　　在图4中,根据实测分析.曲线2上的∈max值。就是锤头对销轴最大反冲击力F2max所引起的线应变。另根据电测原理和转子轴的受力特点，转子轴上测试处的弯矩Mmax为：

　　d为转子轴测试处的直径；B为试验模型中二圆盘间的距离;L为转子轴上二轴承间的距离;E为转子轴材料的弹性模量。
　　根据公式((16)和(24).在单颗粒物料破碎时，逐次改变电机转速和分别加入砂岩、钢球、麻石、石灰岩等不同物料进行了破碎试验。得出了一系列F1max/F1数据。

　　3  F1max/F1值的数据处理和结论
　　从试验获得的一系列数据F1max/F1值可以发现。它呈非线性变化。为了了解其变化规律。利用计算机对F1max/F1的值进行数据处理，它包含均值方差计算和正态性检验等.其结果如图５所示。

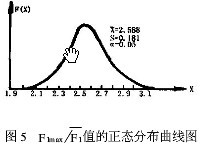
　　根据图5中的数理统计结果。可得如下结论：
　　(1)根据所获数据发现F1max/F1的比值不呈线性变化。由数理统计原理可知F1max/F1比值落在区间[X- 3s,X+ 3s]的概率为99.7%,置信度为:1-α=95%。
　　(2)因为X- 3s=2.045,X+ 3s= 3.128,根据概率论的观点。可得到F1max/F1值的实验公式为:

　　式中。F1为平均破碎力.按公式((16)计算。